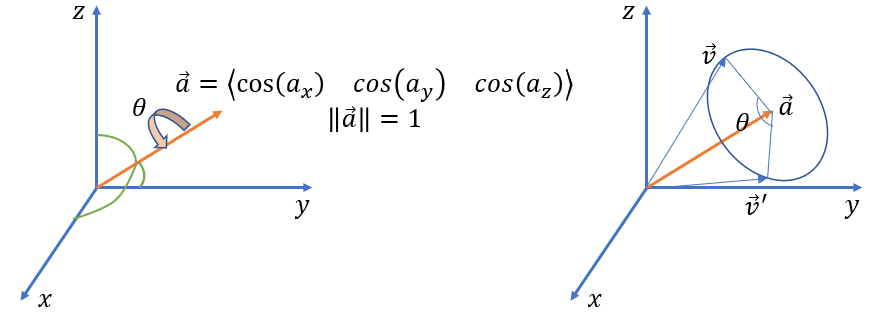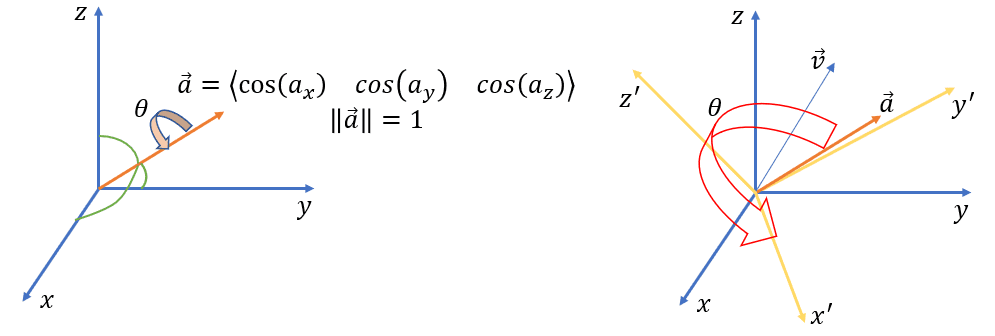AHRS Quaternions and Rotations
Quaternions
Quaternion은 사원수 또는 쿼터니언이라고 부르며, 복소수를 확장해 만든 수 체계입니다.
i2=j2=k2=ijk=−1q=xi+yj+zk+wq=[xyzw]T
Norm
q=x2+y2+z2+w2
Conjugate quaternion
qˉ=−xi−yj−zk+w
pq=qˉpˉ
Pure quaternion
q=[xyz0]T
Identity quaternion
I��=[0001]T
Inverse quaternion
q−1=∣∣q∣∣2qˉ(q−1=qˉif ||q|| = 1)
Hamilton product
pq=L(p)q=R(q)p=pwpz−py−px−pzpwpx−pypy−pxpw−pzpxpypzpwqxqyqzqw=qw−qzqy−qxqzqw−qx−qy−qyqxqw−qzqxqyqzqwpxpypzpw
Rotations
Rotate Vector
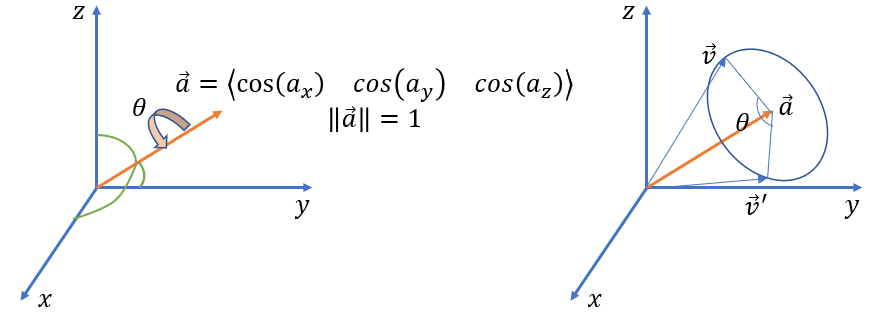
a(∣∣a∣∣=1)를 기준으로 벡터를 θ만큼 회전시키는 데 필요한 쿼터니언은 아래와 같습니다.
q(a,θ)=[asin(2θ)cos(2θ)]T
벡터와 쿼터니언 연산 시 벡터는 pure quaternioin으로 나타낼 수 있습니다.
v=vxi+vyj+vzk
v=[vxvyvz0]
a(∣∣a∣∣=1)를 기준으로 v를 θ만큼 회전시킨 v′를 구하는 식은 아래와 같습��니다.
v′v′=qvqˉ=R(qˉ)L(q)v=1−2(qy2+qz2)2(qxqy+qzqw)2(qxqz−qyqw)02(qxqy−qzqw)1−2(qx2+qz2)2(qyqz+qxqw)02(qxqz+qyqw)2(qyqz−qxqw)1−2(qx2+qy2)00001vxvyvz0
연속적인 회전은 아래와 같이 구할 수 있습니다.
v1v2v3⋮===q01v0qˉ01q12v1qˉ12q23v2qˉ23⋮==q12q01v0qˉ01qˉ12q23q12q01v0qˉ01qˉ12qˉ23⋮
vk=qk−1kqk−2k−1⋯q01v0qˉ01⋯qˉk−2k−1qˉk−1k
q0k=qk−1kqk−2k−1⋯q01
Rotate Frame
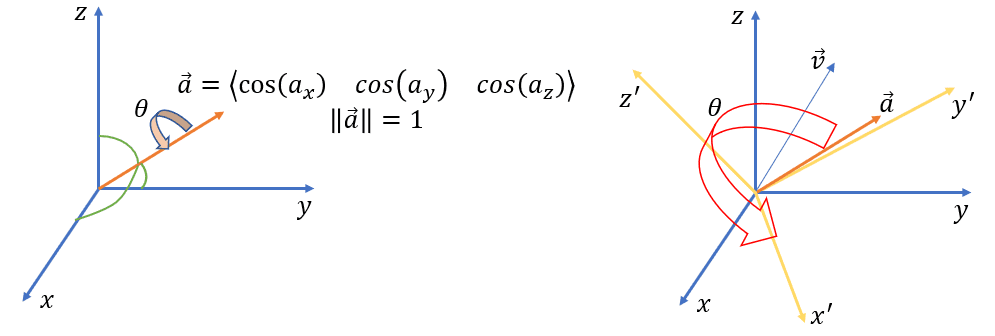
처음에 A와 B 좌표계는 동일했다가 B 좌표계가 a(∣∣a∣∣=1)를 기준으로 θ만큼 회전했다고 가정하겠습니다.
Av는 A에서 관찰한 v입니다. Av는 회전하기 전 B 좌표계에서 관찰한 v라고 생각할 수도 있습니다.
Bv는 회전 후 B에서 관찰한 v입니다.
B 좌표계 위에 있는 관찰자 입장에서 보면 Av가 a를 기준으로 −θ만큼 회전하여 Bv가 되었다고 생각할 수 있습니다.
반대로 Bv가 a를 기준으로 θ만큼 회전하면 Av라고 생각할 수 있습니다.
Vector 회전식을 이용하여 Av와 Bv의 관계를 식으로 나타내면 아래와 같습니다.
을
Av=q(Bv)qˉ=qBA(Bv)qˉBA=1−2(qy2+qz2)2(qxqy+qzqw)2(qxqz−qyqw)02(qxqy−qzqw)1−2(qx2+qz2)2(qyqz+qxqw)02(qxqz+qyqw)2(qyqz−qxqw)1−2(qx2+qy2)00001BvxBvyBvz0
연속적인 회전은 아래와 같이 구할 수 있습니다.
k−1vk−2vk−3v⋮===qkk−1kvqˉkk−1qk−1k−2k−1vqˉk−1k−2qk−2k−3k−2vqˉk−2k−3⋮==qk−1k−2qkk−1kvqˉkk−1qˉk−1k−2qk−2k−3qk−1k−2qkk−1kvqˉkk−1qˉk−1k−2qˉk−2k−3⋮
0v=q10q21⋯qkk−1kvqˉkk−1⋯qˉ21q�ˉ10
qk0=q10q21⋯qkk−1
Small angle approximation
Taylor Series에 의해 sin함수와 cos함수는 아래와 같은 다항식으로 나타낼 수 있습니다.
sin2θcos2θ=2θ−3!1(2θ)3+5!1(2θ)5−⋯=1−2!1(2θ)2+4!1(2θ)4−⋯
θ→0 라고 가정하면 sin함수와 cos함수는 아래와 같이 나타낼 수 있습니다.
sin2θcos2θ≈2θ≈1
따라서 회전각이 충분히 작을 때, 회전 쿼터니언은 아래와 같이 나타낼 수 있습니다.
q(a,θ)=[asin(2θ)cos(2θ)]T≈[2θa1]T(θ→0)