AHRS Sensor Calibration

Accelerometer calibration

감도 오차는 없다고 가정하고 오프셋만 계산합니다.

센서의 한 축을 지표에 수직인 방향과 나란하게 맞춥니다.
움직임이나 진동이 측정되지 않도록 센서를 고정합니다.
가속도 값을 여러번 측정하여 평균을 구합니다.
지표에 수직인 방향과 나란한 축은 센서의 1 g에 해당하는 값과 비교하여 오프셋을 구합니다.
다른 축은 측정된 평균 값이 오프셋 입니다.

Example

HAL_StatusTypeDef mpu9250_acc_calibration(void) {
    int16_t           raw_acc[3];
    int32_t           raw_acc_sum[3] = {0};
    HAL_StatusTypeDef status;

    for(int16_t i = 0; i < 256; ++i) {
        status = mpu9250_read_3_axis(MPU9250_ACCEL_XOUT_H, raw_acc);
        if(status != HAL_OK) { return status; }
        raw_acc_sum[0] += raw_acc[0];
        raw_acc_sum[1] += raw_acc[1];
        raw_acc_sum[2] += raw_acc[2];
        delay_ms(2);
    }

    acc_offset[0] = raw_acc_sum[0] >> 8;
    acc_offset[1] = raw_acc_sum[1] >> 8;
    acc_offset[2] = raw_acc_sum[2] >> 8;

    // An axis must be parallel to vertical.
    for(int16_t i = 0; i < 3; ++i) {
        if(acc_offset[i] > acc_1G_FS * 0.9) {
            acc_offset[i] -= acc_1G_FS;
        } else if(acc_offset[i] < -acc_1G_FS * 0.9) {
            acc_offset[i] += acc_1G_FS;
        }
    }

    return HAL_OK;
}

Gyroscope calibration

감도 오차는 없다고 가정하고 오프셋만 계산합니다.

움직임이나 진동이 측정되지 않도록 센서를 고정합니다.
각속도 값을 여러번 측정하여 평균을 구합니다.
측정된 평균 값이 오프셋 입니다.

Example

HAL_StatusTypeDef mpu9250_gyro_calibration(void) {
    int16_t           raw_gyro[3];
    int32_t           raw_gyro_sum[3] = {0};
    HAL_StatusTypeDef status;

    for(int16_t i = 0; i < 256; ++i) {
        status = mpu9250_read_3_axis(MPU9250_GYRO_XOUT_H, raw_gyro);
        if(status != HAL_OK) { return status; }
        raw_gyro_sum[0] += raw_gyro[0];
        raw_gyro_sum[1] += raw_gyro[1];
        raw_gyro_sum[2] += raw_gyro[2];
        delay_ms(2);
    }

    gyro_offset[0] = raw_gyro_sum[0] >> 8;
    gyro_offset[1] = raw_gyro_sum[1] >> 8;
    gyro_offset[2] = raw_gyro_sum[2] >> 8;

    return HAL_OK;
}

Magnetometer calibration

오프셋만 있다고 가정하는 경우, 감도 오차와 오프셋이 있다고 가정하는 경우만 생각해서 계산합니다. 두 경우 모두 최소자승법(least squares method)을 사용하게 됩니다.

자기장의 경우 위치와 시간에 따라 변하지만 측정하는 동안에는 변하지 않는다고 가정합니다.

센서를 여러방향으로 회전시키며 데이터를 측정할 때 생기는 그래프를 구체라고 가정하면 오프셋만 있는 경우이고, 회전하지 않은 타원체라고 가정하면 감도 오차와 오프셋이 있는 경우입니다.

구체라고 가정한 경우 식은 아래와 같습니다.

m^2_x + m^2_y + m^2_z + am_x + bm_y + cm_z = d

am_x + bm_y + cm_z - d = -(m^2_x + m^2_y + m^2_z)

\left(m_x - {-a \over 2}\right)^2 + \left(m_y - {-b \over 2}\right)^2 + \left(m_z - {-c \over 2}\right)^2 = d + \left( a \over 2 \right)^2 + \left( b \over 2 \right)^2 + \left( c \over 2 \right)^2

회전하지 않은 타원체라고 가정한 경우 식은 아래와 같습니다.

am^2_x+bm^2_y+cm^2_z+dm_x+em_y+fm_z=1

\begin{aligned} \left( m_x - {-d \over 2a} \right)^2 + \left( m_y - {-e \over 2b} \over \sqrt {a \over b} \right)^2 & + \left( m_z - {-f \over 2c} \over \sqrt {a \over c} \right)^2 \\ & = {1000 \over a} +\left( d \over 2a \right)^2 + {b \over a}\left( e \over 2b \right)^2 + {c \over a}\left( f \over 2c \right)^2 \end{aligned}

Least squares method

수식 전개는 회전하지 않은 타원체 기준으로 하겠습니다.

n회 측정된 데이터를 행렬식으로 나타내면 식 (1)과 같습니다.

Mx= \left[ \begin{matrix} m^2_{x,1} & m^2_{y,1} & m^2_{z,1} & m_{x,1} & m_{y,1} & m_{z,1} \\ m^2_{x,2} & m^2_{y,2} & m^2_{z,2} & m_{x,2} & m_{y,2} & m_{z,2} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ m^2_{x,n} & m^2_{y,n} & m^2_{z,n} & m_{x,n} & m_{y,n} & m_{z,n} \end{matrix} \right] \left[ \begin{matrix} a \\ b \\ c \\ d \\ e \\ f \end{matrix} \right] = \left[ \begin{matrix} 1 \\ 1 \\ \vdots \\ \vdots \\ \vdots \\ 1 \end{matrix} \right] = c \tag{1}

$x$ 를 구해야 하는데, $M$ 의 역행렬을 구할 수 없기 때문에 최소자승법을 사용하게 됩니다. 최소자승법은 오차 제곱의 합을 최소화 하는 것이므로 수식은 아래와 같이 유도할 수 있습니다.

{\partial\over\partial c} \left( \begin{Vmatrix} c-Mx \end{Vmatrix}^2 \right) = -2M^T \left( c - Mx \right) = 0

M^T Mx = M^T c \tag{2}

M^TM= \sum_{k=1}^n \left[ \begin{matrix} m^4_{x,k} & m^2_{x,k}m^2_{y,k} & m^2_{x,k}m^2_{z,k} & m^3_{x,k} & m^2_{x,k}m_{y,k} & m^2_{x,k}m_{z,k} \\ & m^4_{y,k} & m^2_{y,k}m^2_{z,k} & m^2_{y,k}m_{x,k} & m^3_{y,k} & m^2_{y,k}m_{z,k} \\ & & m^4_{z,k} & m^2_{z,k}m_{x,k} & m^2_{z,k}m_{y,k} & m^3_{z,k} \\ & & & m^2_{x,k} & m_{x,k}m_{y,k} & m_{x,k}m_{z,k} \\ &symmetric& & & m^2_{y,k} & m_{y,k}m_{z,k} \\ & & & & & m^2_{z,k} \end{matrix} \right]

M^Tc= \sum_{k=1}^n \left[ \begin{matrix} m^2_{x,k} & m^2_{y,k} & m^2_{z,k} & m_{x,k} & m_{y,k} & m_{z,k} \end{matrix} \right]^T

x = \left( M^T M \right)^{-1} M^T c \tag{3}

식 (3)을 사용하여 계수를 구할 수 있습니다.

Cholesky decomposition

식 (3)을 계산하기 위해 역행렬을 구해야합니다. 역행렬 계산을 피하기 위해 Cholesky decomposition을 사용하게 됩니다. 분해 알고리즘은 Cholesky–Banachiewicz algorithm을 사용했습니다.

팁

Cholesky decomposition 외에 QR decomposition, SVD decomposition, Gaussian elimination 등 다양한 방법을 사용할 수 있습니다.

M^T M = L L^*\text{(Cholesky decomposition)}

L L^*x = Ly = M^T c \tag{4}

L^*x=y \tag{5}

식 (4)에 forward substitution을 적용하여 $y$ 를 구하고, 식 (5)에 backward substitution을 적용하면 $x$ 를 구할 수 있습니다.

교정 전 후 측정된 데이터 그래프입니다. 파란색 데이터가 교정 전, 빨간색 데이터가 교정 후 입니다.

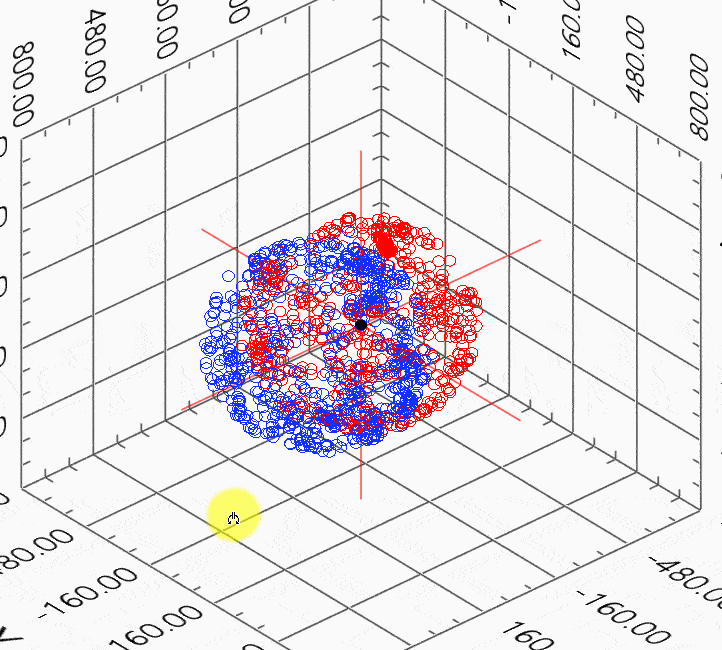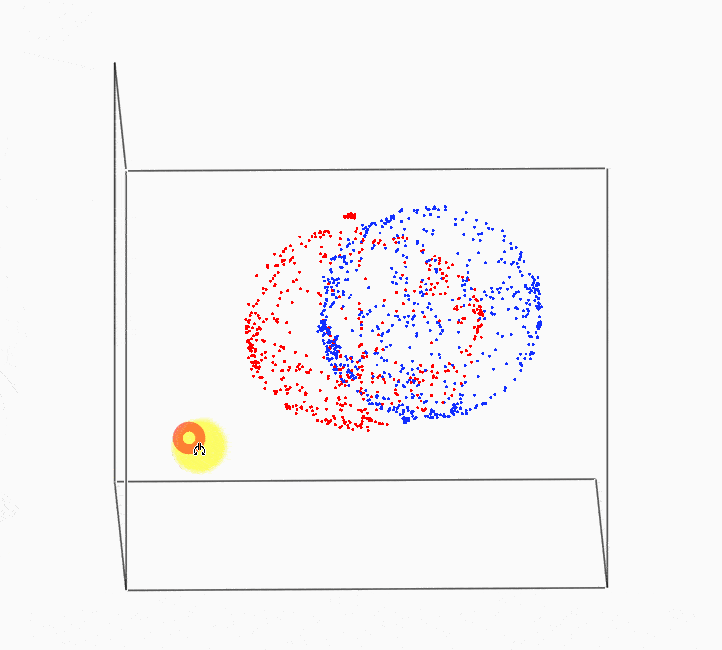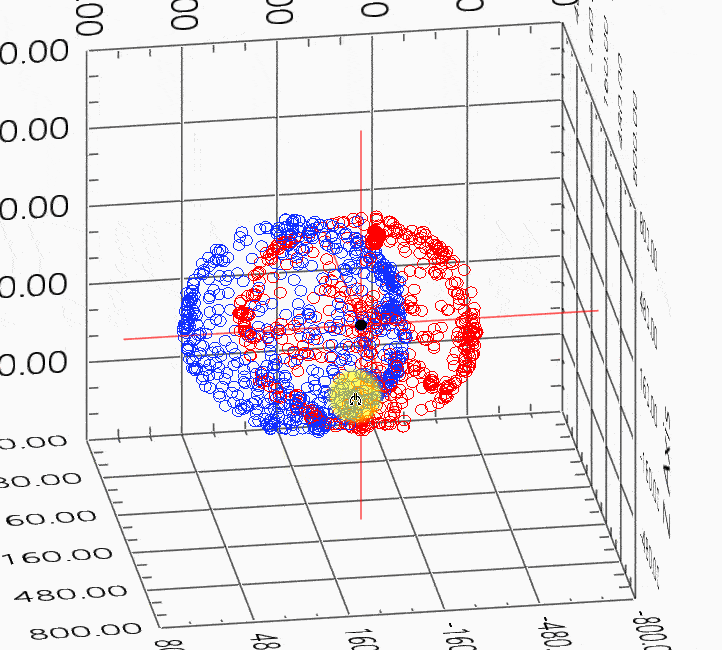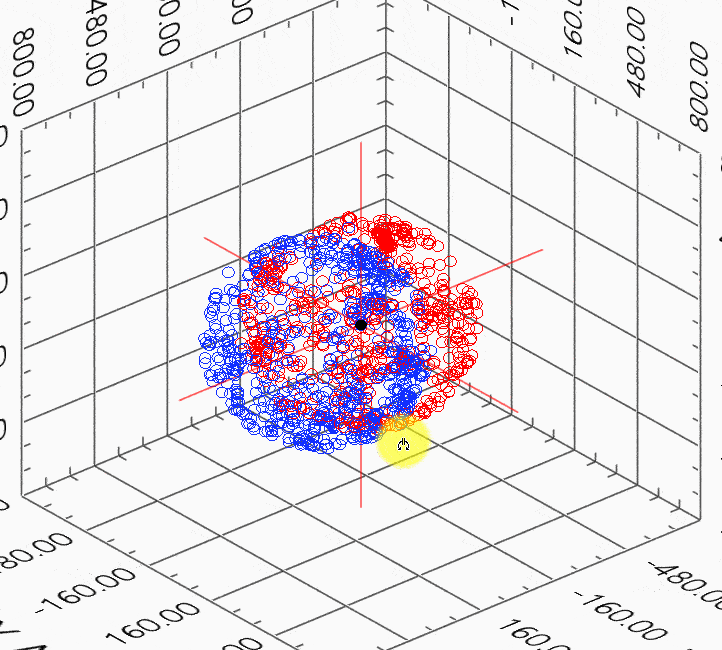
Examples

Ellipsoid
Sphere

#include <math.h>

HAL_StatusTypeDef mpu9250_mag_calibration(void) {
    HAL_StatusTypeDef status;
    int16_t           raw_mag[3];
    uint8_t           temp[6];
    double            component[6];
    double            sigma_A[21] = {0};
    double            sigma_b[6]  = {0};

    // M^t * M * coef = M^t * 1[k:1]
    // sA * coef = sb
    // ax^2 + by^2 + cz^2 + dx + ey + fz = 1
    for(int16_t k = 0; k < 100; ++k) {
        status = mpu9250_read_3_axis(MPU9250_EXT_SENS_DATA_00, raw_mag);
        if(status != HAL_OK) { return status; }
        component[3] = raw_mag[0];
        component[4] = raw_mag[1];
        component[5] = raw_mag[2];
        component[0] = component[3] * component[3];
        component[1] = component[4] * component[4];
        component[2] = component[5] * component[5];

        // Lower triangular matrix
        for(int16_t i = 0; i < 6; ++i) {
            temp[i] = i * (i + 1) >> 1;    // row
            for(int16_t j = 0; j < i + 1; ++j) {
                sigma_A[temp[i] + j] += component[i] * component[j];
            }
            sigma_b[i] += component[i];
        }

        delay_ms(200);
    }

    // Cholesky decomposition
    // sA = L * L^t
    for(int16_t i = 0; i < 6; ++i) {
        for(int16_t j = 0; j < i + 1; ++j) {
            if(i == j) {
                sigma_A[temp[i] + i] = sqrt(sigma_A[temp[i] + i]);
            } else {
                for(int16_t k = 0; k < j; ++k) {
                    sigma_A[temp[i] + j]
                        -= sigma_A[temp[i] + k] * sigma_A[temp[j] + k];
                }
                sigma_A[temp[i] + j] /= sigma_A[temp[j] + j];
                sigma_A[temp[i] + i]
                    -= sigma_A[temp[i] + j] * sigma_A[temp[i] + j];
            }
        }
    }

    // L * ( L^t * coef ) = b
    // L * x = b
    // component == x
    for(int16_t i = 0; i < 6; ++i) {
        for(int16_t j = 0; j < i; ++j) {
            sigma_b[i] -= sigma_A[temp[i] + j] * component[j];
        }
        component[i] = sigma_b[i] / sigma_A[temp[i] + i];
    }

    // L^t * coef = x
    // component == x
    // sigma_b == coef
    for(int16_t i = 5; i >= 0; --i) {
        for(int16_t j = 5; j > i; --j) {
            component[i] -= sigma_A[temp[j] + i] * sigma_b[j];
        }
        sigma_b[i] = component[i] / sigma_A[temp[i] + i];
    }

    mag_offset[0]      = (-sigma_b[3] / sigma_b[0]) / 2;
    mag_offset[1]      = (-sigma_b[4] / sigma_b[1]) / 2;
    mag_offset[2]      = (-sigma_b[5] / sigma_b[2]) / 2;
    mag_sensitivity[0] = 1;
    mag_sensitivity[1] = sqrt(sigma_b[1] / sigma_b[0]);
    mag_sensitivity[2] = sqrt(sigma_b[2] / sigma_b[0]);

    return HAL_OK;
}

Accelerometer calibration​

Example​

Gyroscope calibration​

Example​

Magnetometer calibration​

Least squares method​

Cholesky decomposition​

Examples​

Accelerometer calibration

Example

Gyroscope calibration

Example

Magnetometer calibration

Least squares method

Cholesky decomposition

Examples