본문으로 건너뛰기

Neural Network

Neuron(Perceptron)​

zjl=∑kωjklakl−1+bjlz^l_j = \sum_k{\omega^l_{jk}a^{l-1}_k} + b^l_j ajl=σ(zjl)a^l_j = \sigma\left(z^l_j\right)

Loss function​

L2 loss function​

Loss≡12∥y−aL∥2=12∑i(yi−aiL)2Loss \equiv \frac{1}{2} \lVert \mathbf{y} - \mathbf{a}^L \rVert^2 = \frac{1}{2} \sum_i{\left(y_i - a^L_i\right)^2} Loss≥0(y 는 주어진 답)Loss \geq 0 \quad \left(\mathbf{y}\text{ 는 주어진 답}\right)

Neural Network Training​

Neural Network Training을 통해 찾아야 할 것은 LossLoss의 결과를 최소화하기 위한 weights와 biases입니다. w\mathbf{w} 가 weights와 biases를 나타내는 벡터일 때,

Lossnext=Loss+ΔLoss≈Loss+∇Loss⋅ΔwLoss_{next} = Loss + \Delta Loss \approx Loss + \nabla Loss \cdot \Delta \mathbf{w}

LossLoss는 감소해야하기 때문에, 반드시 ∇Loss⋅Δw<0\nabla Loss \cdot \Delta \mathbf{w} < 0 조건을 만족해야합니다. 따라서 Δw\Delta \mathbf{w}는 아래와 같이 결정 될 수 있습니다.

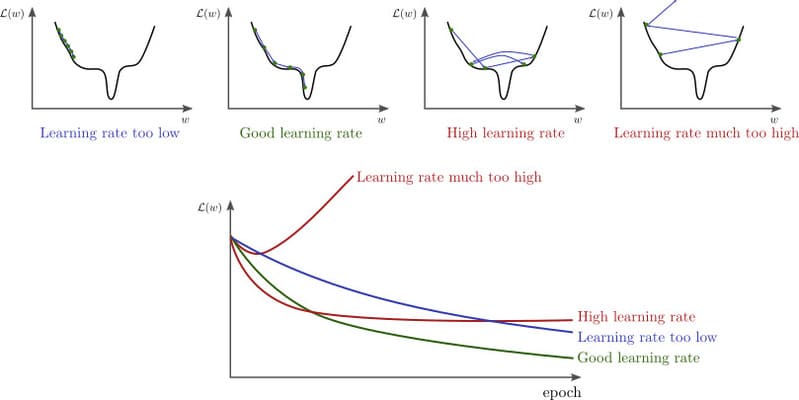
Δw=−η∇Loss=−ϵ∇Loss∥∇Loss∥(ϵ>0)\Delta \mathbf{w} = - \eta \nabla Loss = - \epsilon \frac{\nabla Loss}{\lVert \nabla Loss \rVert} \quad ( \epsilon > 0)

η\eta는 learning rate이고, ϵ\epsilon은 step입니다. 만약 step이 너무 크다면, LossLoss는 발산하고, 너무 작으면, 수렴속도가 느려집니다. 따라서 적절한 값을 설정하는 것이 중요합니다.

Δw\Delta \mathbf{w} 이 결정되면, wnext\mathbf{w}_{next}은 아래와 같이 결정됩니다.

wnext=w+Δw\mathbf{w}_{next} = \mathbf{w} + \Delta \mathbf{w}

Stochastic Gradient Descent(SGD)​

∇Loss=1n∑x∇Lossx\nabla Loss = \frac{1}{n}\sum_x{\nabla Loss_x}

훈련을 위한 데이터셋이 큰 경우, 시간이 많이 걸릴 수 있습니다. 전체 데이터셋에서 랜덤으로 데이터를 선택해 만든 데이터셋 X1,X2,...,XmX_1, X_2, ..., X_m 을 mini-batch라고 하는데, 이 mini-batch가 전체 데이터 셋의 분포와 유사하다고 가정하면 아래와 같은 식이 성립합니다.

∇Loss=1n∑x∇Lossx≈1m∑i=1m∇LossXi\nabla Loss = \frac{1}{n}\sum_x{\nabla Loss_x} \approx \frac{1}{m}\sum^m_{i=1}{\nabla Loss_{X_i}}
  • batch 크기가 줄어 한 step을 계산하는데 걸리는 시간이 줄어듭니다.
  • 수렴하는 데 필요한 step 수가 증가합니다.
  • mini-batch의 크기가 작을 수록 batch의 분포가 전체 데이터 셋의 분포와 달라질 확률이 높기 때문에 학습이 불안정해집니다.
  • (계산 시간/step) * (수렴에 필요한 step)을 학습 시간이라고 하면, 학습 시간이 최소가 되는 batch 크기가 존재합니다.

Forward-propagation​

Forward-propagation (or forward pass)는 입력부터 출력으로 이어지는 네트워크를 순서대로 계산하고 그 결과를 저장하는 과정을 말합니다.

Back-propagation​

zjl=∑kωjklakl−1+bjlz^l_j = \sum_k{\omega^l_{jk}a^{l-1}_k} + b^l_j ajl=σ(zjl)a^l_j = \sigma\left(z^l_j\right)

LossLoss를 직접 미분하기 어렵기 때문에, Back-propagation을 사용하여 ∇Loss\nabla Loss를 계산합니다.

ll 레이어의 jj 뉴런의 에러 δjl\delta^l_j 는 아래와 같이 정의됩니다.

δjl≡∂Loss∂zjl\delta^l_j \equiv \frac{\partial Loss}{\partial z^l_j}

zjlz^l_j는 forward propagation을 통해 계산된 값이므로, δl+1\mathbf{\delta}^{l+1}를 안다면, δjl\delta^l_j를 아래와 같이 구할 수 있습니다.

δjl=∂Loss∂zjl=∑i∂Loss∂zil+1∂zil+1∂zjl(∂zil+1∂zjl=ωijl+1 σ′(zjl))=∑i∂Loss∂zil+1ωijl+1 σ′(zjl)=∑iδil+1ωijl+1 σ′(zjl)\begin{aligned} \delta^l_j = \frac{\partial Loss}{\partial z^l_j} & = \sum_i{\frac{\partial Loss}{\partial z^{l+1}_i} \frac{\partial z^{l+1}_i}{\partial z^l_j}} \quad \left( \frac{\partial z^{l+1}_i}{\partial z^l_j} = \omega^{l+1}_{ij} \, \sigma' \left(z^l_j\right) \right)\\ & = \sum_i{\frac{\partial Loss}{\partial z^{l+1}_i} \omega^{l+1}_{ij} \, \sigma' \left(z^l_j\right)} \\ & = \sum_i{\delta^{l+1}_i \omega^{l+1}_{ij} \, \sigma' \left(z^l_j\right)} \end{aligned}

L2 loss를 사용한다면, ajLa^L_j는 forward propagation을 통해 구할 수 있고 δjL=(ajL−yj) σ′(zjL)\delta^L_j = (a^L_j - y_j) \, \sigma' \left( z^L_j \right) 이므로, 아래와 같이 에러를 구할 수 있습니다.

δjL=(ajL−yj) σ′(zjL)\delta^L_j = (a^L_j - y_j) \, \sigma' \left( z^L_j \right) δjL−1=∑iδiLωijL σ′(zjL−1)⋮\delta^{L-1}_j = \sum_i{ \delta^L_i \omega^L_{ij} \, \sigma' \left(z^{L-1}_j\right)} \\ \vdots

결과적으로 ∇Loss\nabla Loss는 위 식들을 통해 아래와 같이 구할 수 있습니다.

∂Loss∂bjl=∂Loss∂zjl∂zjl∂bjl=δjl\frac{\partial Loss}{\partial b^l_j} = \frac{\partial Loss}{\partial z^l_j} \frac{\partial z^l_j}{\partial b^l_j} = \delta^l_j ∂Loss∂ωjkl=∂Loss∂zjl∂zjl∂ωjkl=δjlakl−1\frac{\partial Loss}{\partial \omega^l_{jk}} = \frac{\partial Loss}{\partial z^l_j} \frac{\partial z^l_j}{\partial \omega^l_{jk}} = \delta^l_j a^{l-1}_k

Training​

초기 weights and biases를 랜덤하게 설정하고, Forward-propagation -> Back-propagation -> weights and biases update를 반복하는 것을 Training이라고 합니다. LossLoss가 더이상 작아질 수 없다고 판단될 때, weights and biases 값이 최종 결과물이 됩니다.

Initialization​

입력의 분산보다 출력의 분산이 커지면 활성화 함수에 따라 수렴하는 부분이 생길 수 있고, 이것은 Vanishing gradient 문제를 야기할 수 있습니다.

변수를 적절히 초기화 해주는 것은 Vanishing gradient, Exploding gradient 등의 문제 해결에 도움이 되고, 훈련속도를 높일 수 있습니다.

Reference​