본문으로 건너뛰기

Transformer(1706) - Attention Is All You Need

Reference

Transformer​


Figure 1. The Transformer

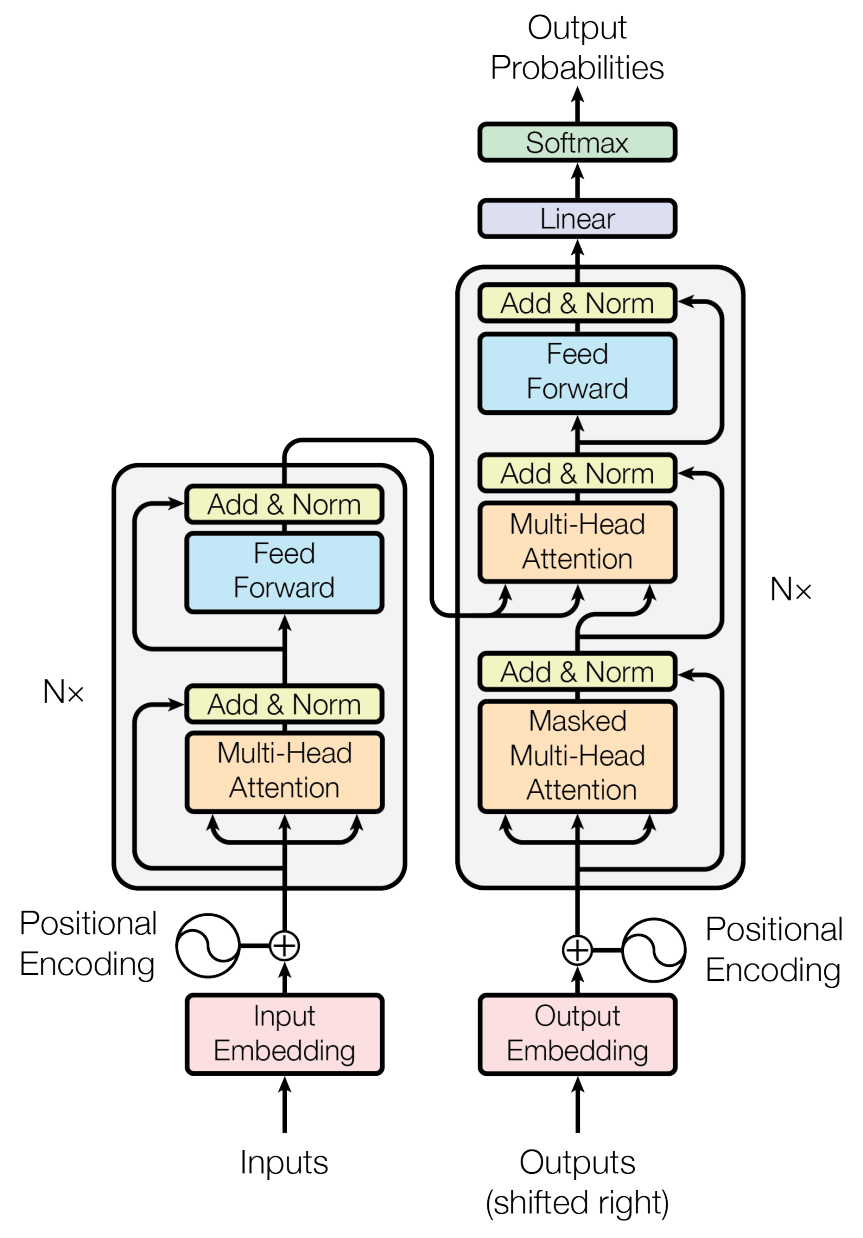
왼쪽의 동일한 Layer를 반복적으로 쌓은 구조가 Encoder이고, 오른쪽의 동일한 Layer를 반복적으로 쌓은 구조가 Decoder입니다. Transformer는 Encoder와 Decoder로 구성되어 있습니다. Encoder는 입력된 문장을 이해하고, Decoder는 이해한 내용을 바탕으로 출력 문장을 생성합니다.

Tokenizer​

Tokenizer는 문장을 입력하면 입력된 문장을 분리하여 토큰(Token)으로 변환합니다.

Input
오늘 날씨 어때?
Output
[128000,  58368, 105622, 105605, 107497, 101139, 106745,     30]

Embedding Layer​

Embedding Layer는 입력된 토큰을 벡터로 변환합니다.

Input
[128000,  58368, 105622, 105605, 107497, 101139, 106745,     30]
Output
[[-1.4305e-04,  1.0777e-04, -1.9646e-04,  ...,  2.0218e-04,  1.4842e-05,  3.0136e-04],
 [-4.7607e-03, -8.0566e-03, -1.2390e-02,  ..., -1.7624e-03, -2.7847e-04, -1.0132e-02],
 [-8.7891e-03,  3.3264e-03,  1.1230e-02,  ..., -5.2185e-03, -4.4250e-03,  1.1414e-02],
 [-2.1667e-03, -5.1270e-03, -3.3417e-03,  ...,  7.2937e-03, -8.5449e-03,  3.9978e-03],
 [-1.4465e-02, -7.5073e-03,  1.2573e-02,  ..., -2.1240e-02,  3.8452e-03,  7.4387e-04],
 [ 7.9956e-03, -1.5991e-02,  4.8828e-03,  ..., -1.6113e-02,  2.9907e-03, -8.2779e-04],
 [-7.3547e-03, -1.9531e-02, -3.9978e-03,  ..., -3.5095e-03,  1.9897e-02,  7.8735e-03],
 [-4.9438e-03, -1.6098e-03,  6.4087e-03,  ...,  1.9989e-03, -1.0147e-03, -4.8523e-03]]

Positional Encoding​

Transformer는 RNN과 달리 입력된 순서에 의해 영향받는 것이 없기 때문에 입력된 순서를 알 수 있도록 Positional Encoding을 만들어 입력 토큰에 추가해야 합니다. 아래는 sin, cos을 활용하여 Positional Encoding을 만드는 예시 입니다.

pi={sin(i100002∗1/d),cos(i100002∗1/d),sin(i100002∗2/d),cos(i100002∗2/d),⋯ }∈Rdp_i = \left\{ sin\left(\frac{i}{10000^{2*1/d}}\right), cos\left(\frac{i}{10000^{2*1/d}}\right), sin\left(\frac{i}{10000^{2*2/d}}\right), cos\left(\frac{i}{10000^{2*2/d}}\right), \cdots \right\} \in \mathbb{R}^{d}

Scaled Dot-Product Attention​


Figure 2. Scaled Dot-Product Attention
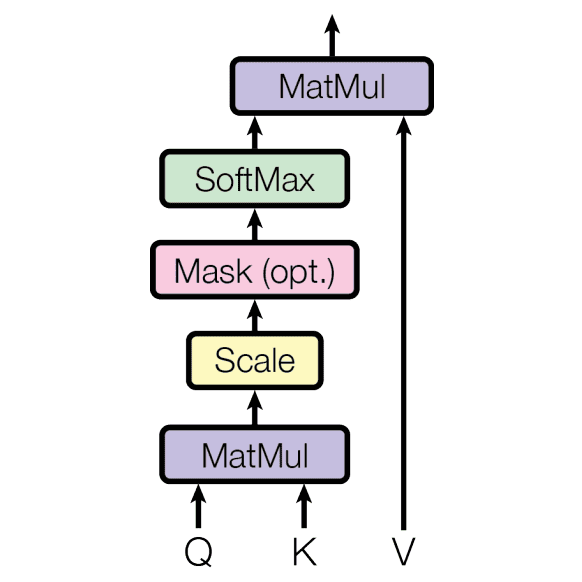
  • Input
    • xi∈Rdx_i \in \mathbb{R}^d
    • X={x1,x2,⋯ ,xn}∈Rn×dX = \left\{ x_1, x_2, \cdots, x_n \right\} \in \mathbb{R}^{n \times d}
  • Query
    • qi=xiWq∈Rdkq_i = x_i W_q \in \mathbb{R}^{d_k}
    • Q=XWq∈Rn×dkQ=X W_q \in \mathbb{R}^{n \times d_k}
  • Key
    • ki=xiWk∈Rdkk_i = x_i W_k \in \mathbb{R}^{d_k}
    • K=XWk∈Rn×dkK = X W_k \in \mathbb{R}^{n \times d_k}
  • Value
    • vi=xiWv∈Rdv_i = x_i W_v \in \mathbb{R}^{d}
    • V=XWv∈Rn×dV = X W_v \in \mathbb{R}^{n \times d}
  • Attention
    • aij=softmax(qiTkjdk)=exp(qiTkjdk)∑j=1nexp(qiTkjdk)a_{ij} = \text{softmax}(\frac{q_i^T k_j}{\sqrt{d_k}}) = \frac{exp(\frac{q_i^T k_j}{\sqrt{d_k}})}{\sum_{j=1}^n exp(\frac{q_i^T k_j}{\sqrt{d_k}})}
    • A=softmax(QKTdk)∈Rn×nA = \text{softmax}(\frac{Q K^T}{\sqrt{d_k}}) \in \mathbb{R}^{n \times n}
  • Output
    • Attention(Q,K,V)=AV∈Rn×d\text{Attention}(Q, K, V) = A V \in \mathbb{R}^{n \times d}

Multi-Head Attention (MHA)​


Figure 2. Multi-Head Attention
  • headi=Attention(QWiQ,KWiK,VWiV) or Attention(Qi,Ki,Vi)∈Rn×dvhead_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V) \text{ or } \text{Attention}(Q_i, K_i, V_i) \in \mathbb{R}^{n \times d_v}
  • H=Concat(head1,head2,⋯ ,headh)∈Rn×(hdv)H = \text{Concat}(head_1, head_2, \cdots, head_h) \in \mathbb{R}^{n \times (h d_v)}
  • MultiHead(Q,K,V)=HWO∈Rn×d\text{MultiHead}(Q,K,V) = H W_O \in \mathbb{R}^{n \times d}

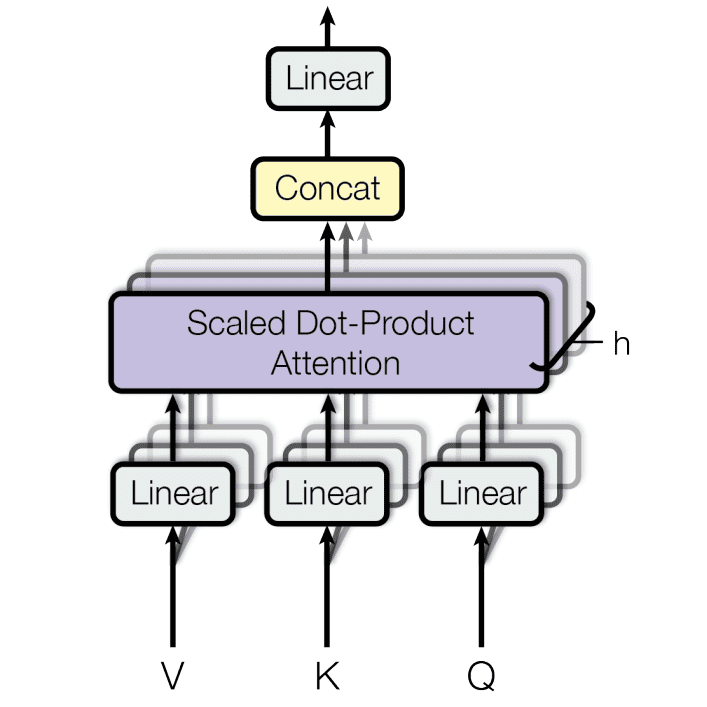
Masked Multi-Head Attention​

[q1k1Tq1k2T⋯q1kmTq2k1Tq2k2T⋯q2kmT⋮⋮⋱⋮qmk1Tqmk2T⋯qmkmT]→mask→[q1k1T−∞⋯−∞q2k1Tq2k2T⋯−∞⋮⋮⋱⋮qmk1Tqmk2T⋯qmkmT]→softmax→[a110⋯0a21a22⋯0⋮⋮⋱⋮an1an2⋯ann]\begin{bmatrix} q_1 k_1^T & q_1 k_2^T & \cdots & q_1 k_m^T \\ q_2 k_1^T & q_2 k_2^T & \cdots & q_2 k_m^T \\ \vdots & \vdots & \ddots & \vdots \\ q_m k_1^T & q_m k_2^T & \cdots & q_m k_m^T \end{bmatrix} \rarr \text{mask} \rarr \begin{bmatrix} q_1 k_1^T & -\infty & \cdots & -\infty \\ q_2 k_1^T & q_2 k_2^T & \cdots & -\infty \\ \vdots & \vdots & \ddots & \vdots \\ q_m k_1^T & q_m k_2^T & \cdots & q_m k_m^T \end{bmatrix} \rarr \text{softmax} \rarr \begin{bmatrix} a_{11} & 0 & \cdots & 0 \\ a_{21} & a_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix}

Cross Attention​

Decoder에서 Cross Attention은 이전 레이어의 출력으로 Query를 만들고 Encoder의 출력으로 Key, Value를 만들어서 계산하는 Attention입니다.

  • Qi=XdecoderWiQ∈Rn×dkQ_i = X_{decoder} W_i^Q \in \mathbb{R}^{n \times d_k}
  • Ki=XencoderWiK∈Rm×dkK_i = X_{encoder} W_i^K \in \mathbb{R}^{m \times d_k}
  • Vi=XencoderWiV∈Rm×dvV_i = X_{encoder} W_i^V \in \mathbb{R}^{m \times d_v}
  • CrossMultiHead(Q,K,V)∈Rn×d\text{CrossMultiHead}(Q, K, V) \in \mathbb{R}^{n \times d}

Feed-Forward Network (FFN)​

  • FFN(X)=ReLU(XW1+b1)W2+b2∈Rn×d\text{FFN}(X) = \text{ReLU}(X W_1 + b_1) W_2 + b_2 \in \mathbb{R}^{n \times d}